Ming-Log's Blog

记录生活中的点点滴滴

0%

动手学深度学习【Pytorch】第6章_卷积神经网络1

发表于 更新于 分类于
本文字数： 7k 阅读时长 ≈ 6 分钟

从全连接到卷积

全连接层主要存在以下问题：

  1. 在使用全连接层处理图像数据时，需要先将图像展平为1维数组，然后再对进行相关的计算，这样做忽略了每个图像的空间结构信息。

  2. 全连接层需要将上下两层的神经元全部相连接，这样会导致参数量非常多。举个例子：图像大小是$100\times100$的图像，再输入隐藏层神经元数量为50的网络中时，产生的权重参数量为$100\times100\times50=500\enspace000$

卷积操作主要有以下两个特性：

  1. 平移不变性：不够检测对象出现再图像中的哪个位置，神经网络的前面几层应该对相同的图像区域具有相似的反应，即为“平移不变性”。
  2. 局部性：神经网络的前面几层应该只探索输入图像中的局部区域，而不过度在意图像中相隔较远的区域的关系，这就是“局部性”原则。最终，可以聚合这些局部特征，以在整个图像级别进行预测。

图像卷积

互相关运算

严格来说，卷积层是个错误的叫法，因为它所表达的运算其实是互相关运算，而不是卷积运算。

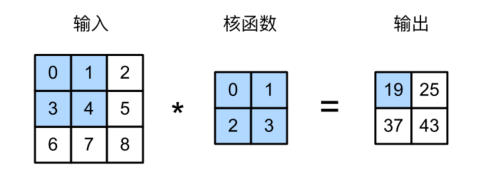
互相关运算_202303092138

输出特征图的大小为$(n_h-k_h+1)\times(n_w-k_w+1)$

其中：

  • $n_h$为原始图像高度
  • $n_w$为原始图像宽度
  • $k_h$为卷积核高度
  • $k_w$为卷积核宽度
1
2
3
import torch
from torch import nn
from d2l import torch as d2l
1
2
3
4
5
6
7
def corr2d(X, K):  #@save
    """计算二位互相关运算"""
    Y = torch.zeros((X.shape[0]-K.shape[0]+1, X.shape[1]-K.shape[1]+1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i:i+K.shape[0], j:j+K.shape[1]] * K).sum()
    return Y
1
2
3
X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
corr2d(X, K)
tensor([[19., 25.],
        [37., 43.]])

卷积层

基于上面定义的corr2d函数实现二维卷积层。在__init__构造函数中，将weight和bias声明为两个模型参数，前向传播函数调用corr2d函数并添加偏置。

1
2
3
4
5
6
7
8
class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super().__init__()
        self.weight = nn.Parameter(torch.rand(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1,))
        
    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

使用$2\times2$的卷积核对$X$进行卷积

1
Conv2D((2, 2))(X)
tensor([[2.8595, 4.4158],
        [7.5284, 9.0847]], grad_fn=<AddBackward0>)

图像中的边缘检测

首先我们构造一个6$\times$8像素的黑白图像。中间四列为黑色(0)，其余像素为白色(1)。

1
2
3
X = torch.ones((6, 8))
X[:, 2:6] = 0
X
tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.]])

接下来我们构造一个高度为1，宽度为2的卷积核

1
K = torch.tensor([[1.0, -1.0]])
1
2
Y = corr2d(X, K)
Y
tensor([[ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.]])

其中1代表从白色到黑色的边缘，-1代表从黑色到白色的边缘

接下来将图像进行转置，再次使用上方的卷积核K进行边缘检测

1
corr2d(X.t(), K)
tensor([[0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.]])

我们发现卷积核K只能够检测出垂直边缘，水平边缘无法检测到。

学习卷积核

如果我们只需寻找黑白边缘，那么以上$[1, -1]$的边缘检测器足以。然而，当有了更复杂数值的卷积核，或者连续的卷积层时，我们不可能手动设计滤波器。那么我们是否可以学习由X生成Y的卷积核呢?

现在让我们看看是否可以通过仅查看“输入-输出”对来学习由X生成Y的卷积核。我们先构造⼀个卷积层，并将其卷积核初始化为随机张量。接下来，在每次迭代中，我们⽐较Y与卷积层输出的平⽅误差，然后计算梯度来更新卷积核。为了简单起⻅，我们在此使⽤内置的⼆维卷积层，并忽略偏置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 构造一个二维卷积层，它具有1个输出通道和形状为(1, 2)的卷积核
conv2d = nn.Conv2d(1, 1, kernel_size=(1, 2), bias=False)

# 这个二维卷积层使用四维输入和输出格式(批量大小，通道，高度，宽度)
# 其中批量大小和通道数都为1
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 3e-2  # 学习率

for i in range(10):
    Y_hat = conv2d(X)
    l = (Y_hat - Y) ** 2
    conv2d.zero_grad()
    l.sum().backward()
    # 迭代卷积核
    conv2d.weight.data[:] -= lr * conv2d.weight.grad
    if (i + 1) % 2 == 0:
        print(f'epoch{i+1}, loss{l.sum():.3f}')
epoch2, loss1.894
epoch4, loss0.345
epoch6, loss0.069
epoch8, loss0.016
epoch10, loss0.005

在迭代10此后，误差已经足够低了。看看训练效果

1
conv2d.weight.data.reshape((1, 2))
tensor([[ 0.9989, -0.9873]])

发现得到的结果十分接近前面的卷积核K

填充和步幅

假设以下情景：有时，在应⽤了连续的卷积之后，我们最终得到的输出远⼩于输⼊⼤⼩。这是由于卷积核的宽度和⾼度通常⼤于1所导致的。⽐如，⼀个240×240像素的图像，经过10层5×5的卷积后，将减少到200×200像素。如此⼀来，原始图像的边界丢失了许多有⽤信息。⽽填充是解决此问题最有效的⽅法。有时，我们可能希望⼤幅降低图像的宽度和⾼度。例如，如果我们发现原始的输⼊分辨率⼗分冗余。步幅则可以在这类情况下提供帮助。

填充（padding）

在应⽤多层卷积时，我们常常丢失边缘像素。由于我们通常使⽤⼩卷积核，因此对于任何单个卷积，我们可能只会丢失⼏个像素。但随着我们应⽤许多连续卷积层，累积丢失的像素数就多了。

解决这个问题的⽅法为填充（padding）：在输⼊图像的边界填充元素（通常填充元素是0）。

我们将3×3输⼊填充到5×5，那么它的输出就增加为4×4。阴影部分是第⼀个输出元素以及⽤于输出计算的输⼊和核张量元素：0×0+0×1+0×2+0×3=0。

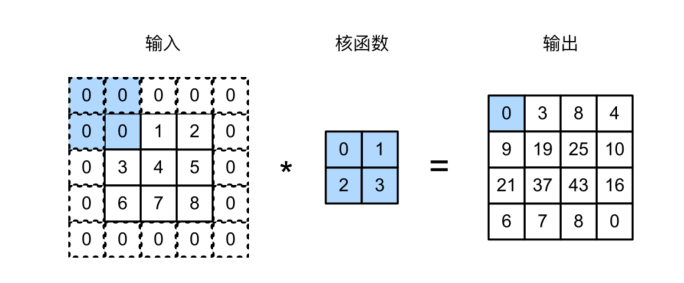
填充_202303092138

通常，如果我们添加$p_h$行填充（大约一半在顶部，一半在底部）和$p_w$列填充（左侧大约一半，右侧一半），则输出形状将为

这意味着输出的高度和宽度将分别增加$p_h$和$p_w$

在许多情况下，我们需要设置$p_h=k_h-1$和$p_w=k_w-1$，使输入和输出具有相同的高度和宽度。这样可以在构建网络时更容易地预测每个图层的输出形状。假设$k_h$是奇数，我们将在高度的两侧填充$p_h/2$行。如果$k_h$是偶数，则一种可能性是在输入顶部填充$(p_h+1)/2$行，在底部填充$(p_h-1)/2$行。同理，我们填充宽度的两侧。

卷积神经⽹络中卷积核的⾼度和宽度通常为奇数，例如1、3、5或7。选择奇数的好处是，保持空间维度的同时，我们可以在顶部和底部填充相同数量的⾏，在左侧和右侧填充相同数量的列。

1
2
3
4
5
6
7
8
9
10
11
import torch
from torch import nn

# 为了方便起见，我们定义了一个计算卷积层的函数
# 此函数初始化卷积层权重，并对输入和输出提高和缩减相应的维数
def comp_conv2d(conv2d, X):
    # 这里的(1,1)表示批量大小和通道数都是1
    X = X.reshape((1, 1) + X.shape)
    Y = conv2d(X)
    # 省略前两个维度：批量大小和通道
    return Y.reshape(Y.shape[2:])
1
2
3
4
# 请注意，这⾥每边都填充了1⾏或1列，因此总共添加了2⾏或2列
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)
X = torch.rand(size=(8, 8))
comp_conv2d(conv2d, X).shape
torch.Size([8, 8])

发现当卷积核大小设置为(3, 3)时，padding设置为1时，能够保留原始的输入图像维度

当卷积核高度和宽度不同时，我们要想保留原始图像的维度，padding在行和列的填充上也应该不一样。例如，我们使用高度为5，宽度为3的卷积核，高度和宽度两边的填充分别为2和1.

计算方法$\frac{5-1}{2}=2$, $\frac{3-1}{2}=1$

1
2
conv2d = nn.Conv2d(1, 1, kernel_size=(5, 3), padding=(2, 1))
comp_conv2d(conv2d, X).shape
torch.Size([8, 8])

步幅

在计算互相关时，卷积窗⼝从输⼊张量的左上⻆开始，向下、向右滑动。在前⾯的例⼦中，我们默认每次滑动⼀个元素。但是，有时候为了⾼效计算或是缩减采样次数，卷积窗⼝可以跳过中间位置，每次滑动多个元素。

我们将每次滑动元素的数量称为步幅（stride）。

下图是垂直步幅为3，⽔平步幅为2的⼆维互相关运算。

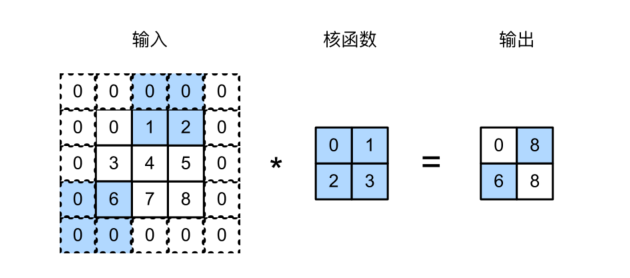
步幅_202303092138

通常，当垂直步幅为$s_h$、⽔平步幅为$s_w$时，输出形状为

如果我们设置了$p_h=k_h-1$和$p_w=k_w-1$，则输出形状将简化为

更进一步，如果输入的高度和宽度可以被垂直和水平步幅整除，则输出形状将为

下面，我们将高度和宽度的步幅设置为2，从而将输入的高度和宽度减半

1
2
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)
comp_conv2d(conv2d, X).shape
torch.Size([4, 4])

接下来看一个稍微复杂一点的例子

1
2
conv2d = nn.Conv2d(1, 1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))
comp_conv2d(conv2d, X).shape
torch.Size([2, 2])

说明:

  • 当输⼊高度和宽度两侧的填充数量分别为$p_h$和$p_w$时，我们称之为填充$(p_h, p_w)$。当$p_h=p_w=p$时，填充是p。
  • 当高度和宽度上步幅分别为$s_h$和$s_w$时，我们称之为步幅(s_h, s_w)。当时的步幅为$s_h=s_w=s$时，步幅为s。

默认情况下，填充为0，步幅为1。在实践中，我们很少使用不一致的步幅或填充，也就是说，我们通常有$p_h=p_w$和$s_h=s_w$。

多输入多输出通道

多输入通道

当输⼊包含多个通道时，需要构造⼀个与输⼊数据具有相同输⼊通道数的卷积核，以便与输⼊数据进⾏互相关运算。

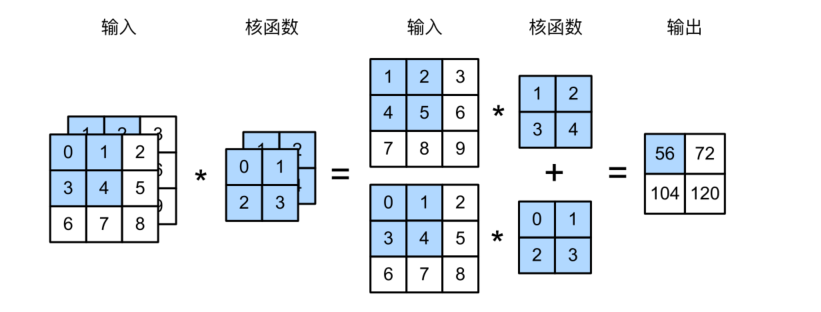
多输入通道_202303092138

1
2
3
def corr2d_multi_in(X, K):
    # 先遍历“X”和“K”的第0个维度（通道维度），再把它们加在一起
    return sum(d2l.corr2d(x,k) for x, k in zip(X, K))
1
2
3
4
5
X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
                  [[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], 
                  [[1.0, 2.0], [3.0, 4.0]]])
corr2d_multi_in(X, K)
tensor([[ 56.,  72.],
        [104., 120.]])

多输出通道

到⽬前为⽌，不论有多少输⼊通道，我们还只有⼀个输出通道。
在最流⾏的神经⽹络架构中，随着神经⽹络层数的加深，我们常会增加输出通道的维数，通过减少空间分辨率以获得更⼤的通道深度。直观地说，我们可以将每个通道看作是对不同特征的响应。⽽现实可能更为复杂⼀些，因为每个通道不是独⽴学习的，⽽是为了共同使⽤⽽优化的。

因此，多输出通道并不仅是学习多个单通道的检测器。

1
2
3
4
def corr2d_multi_in_out(X, K):
    # 迭代“K”的第0个维度，每次都对输入“X”执行互相关运算。
    # 最后将所有结果都叠加在一起
    return torch.stack([corr2d_multi_in(X, k) for k in K], 0)

通过将核张量K与K+1（K中的每个元素加1）和K+2连接起来，构造一个具有3个输出通道的卷积核。

1
2
K = torch.stack((K, K+1, K+2), 0)
K.shape
torch.Size([3, 2, 2, 2])

对输⼊张量X与卷积核张量K执⾏互相关运算。

1
corr2d_multi_in_out(X, K)
tensor([[[ 56.,  72.],
         [104., 120.]],

        [[ 76., 100.],
         [148., 172.]],

        [[ 96., 128.],
         [192., 224.]]])

可以看到第一个通道与之前的结果一致。

1$\times$1卷积层

$1\times1$卷积，即$k_h=k_w=1$，看起来似乎没有多大意义。毕竟卷积的本质是有效提取相邻像素间的相关特征，而$1\times1$卷积显然没有此作用。尽管如此，$1\times1$仍然十分流行，经常包含在复杂深层网络的设计中。

因为使用了最小窗口，$1\times1$卷积失去了卷积层的特有能力—在高度和宽度维度上，识别相邻元素互相作用的能力。其实$1\times1$卷积的唯一计算发生在通道上。

使⽤1×1卷积核与3个输⼊通道和2个输出通道的互相关计算。这⾥输⼊和输出具有相同的⾼度
和宽度，输出中的每个元素都是从输⼊图像中同⼀位置的元素的线性组合。我们可以将1×1卷积层看作是在每个像素位置应⽤的全连接层，以$c_i$个输⼊值转换为$c_o$个输出值。因为这仍然是⼀个卷积层，所以跨像素的权重是⼀致的。同时，1×1卷积层需要的权重维度为$c_o\times c_i$，再额外加上⼀个偏置。

1x1卷积层_202303092138

1
import torch
1
2
3
4
5
6
7
8
def corr2d_multi_in_out_1x1(X, K):
    c_i, h, w = X.shape
    c_o = K.shape[0]
    X = X.reshape((c_i, h * w))
    K = K.reshape((c_o, c_i))
    # 全连接层中矩阵的乘法
    Y = K@X
    return Y.reshape((c_o, h, w))
1
2
X = torch.normal(0, 1, (3, 3, 3))
K = torch.normal(0, 1, (2, 3, 1, 1))
1
2
Y1 = corr2d_multi_in_out_1x1(X, K)
Y1.shape
torch.Size([2, 3, 3])

1
2
Y2 = corr2d_multi_in_out(X, K)
Y2.shape
torch.Size([2, 3, 3])
-------------本文结束感谢您的阅读-------------