动手学深度学习【Pytorch】第6章_卷积神经网络2

汇聚层（Pooling）

通常当我们处理图像时，我们希望逐渐降低隐藏表⽰的空间分辨率、聚集信息，这样随着我们在神经⽹络中层叠的上升，每个神经元对其敏感的感受野（输⼊）就越⼤。

而我们的机器学习任务通常会跟全局图像的问题有关（例如，“图像是否包含⼀只猫呢？”），所以我们最后⼀层的神经元应该对整个输⼊的全局敏感。通过逐渐聚合信息，⽣成越来越粗糙的映射，最终实现学习全局表⽰的⽬标，同时将卷积图层的所有优势保留在中间层。

此外，当检测较底层的特征时（例如 6.2节中所讨论的边缘），我们通常希望这些特征保持某种程度上的平移不变性。例如，如果我们拍摄⿊⽩之间轮廓清晰的图像X，并将整个图像向右移动⼀个像素，即Z[i, j] = X[i, j + 1]，则新图像Z的输出可能⼤不相同。⽽在现实中，随着拍摄⻆度的移动，任何物体⼏乎不可能发⽣在同⼀像素上。即使⽤三脚架拍摄⼀个静⽌的物体，由于快⻔的移动⽽引起的相机振动，可能会使所有物体左右移动⼀个像素（除了⾼端相机配备了特殊功能来解决这个问题）。

本节将介绍汇聚（pooling）层，有时候我们也称为池化层，它具有双重⽬的：

1. 降低卷积层对位置的敏感性

2. 降低对空间降采样表⽰的敏感性。

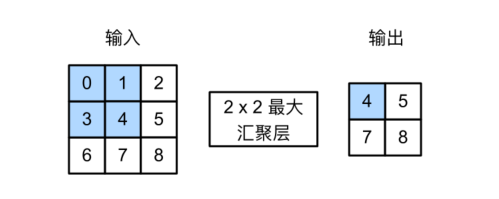
最大汇聚层和平均汇聚层

与互相关运算符⼀样，汇聚窗⼝从输⼊张量的左上⻆开始，从左往右、从上往下的在输⼊张量内滑动。在汇聚窗⼝到达的每个位置，它计算该窗⼝中输⼊⼦张量的最⼤值或平均值。计算最⼤值或平均值是取决于使⽤了最⼤汇聚层还是平均汇聚层。

import torch
from torch import nn
from d2l import torch as d2l

# 步长为1
def pool2d(X, pool_size, mode='max'):
    p_h, p_w = pool_size
    Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            if mode == 'max':
                Y[i, j] = X[i: i + p_h, j: j + p_w].max()
            elif mode == 'avg':
                Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
    return Y

X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
pool2d(X, (2, 2))

tensor([[4., 5.],
        [7., 8.]])

平均汇聚层

pool2d(X, (2, 2), 'avg')

tensor([[2., 3.],
        [5., 6.]])

填充和步幅

与卷积层⼀样，汇聚层也可以改变输出形状。和以前⼀样，我们可以通过填充和步幅以获得所需的输出形状。

X = torch.arange(16, dtype=torch.float32).reshape((1, 1, 4, 4))
X

tensor([[[[ 0.,  1.,  2.,  3.],
          [ 4.,  5.,  6.,  7.],
          [ 8.,  9., 10., 11.],
          [12., 13., 14., 15.]]]])

默认情况下。深度学习框架中的步幅与汇聚窗口的大小相同。因此，如果我们使用形状为(3, 3)的汇聚窗口，那么默认情况下，我们得到的步幅形状为(3, 3)。

pool2d = nn.MaxPool2d(3)
pool2d(X)

tensor([[[[10.]]]])

填充和步幅可以手动设定

pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)

tensor([[[[ 5.,  7.],
          [13., 15.]]]])

可以设定一个任意大小的矩形汇聚窗口，并分别设定填充和步幅的高度和宽度。

pool2d = nn.MaxPool2d((2, 3), stride=(2, 3), padding=(0, 1))
pool2d(X)

tensor([[[[ 5.,  7.],
          [13., 15.]]]])

多个通道

在处理多通道输⼊数据时，汇聚层在每个输⼊通道上单独运算，⽽不是像卷积层⼀样在通道上对输⼊进⾏汇总。这意味着汇聚层的输出通道数与输⼊通道数相同。下⾯，我们将在通道维度上连结张量X和X + 1，以构建具有2个通道的输⼊。

X四维度尺寸意义：（批量大小，通道数，高度， 宽度）

X = torch.cat((X, X + 1), 1)
X

tensor([[[[ 0.,  1.,  2.,  3.],
          [ 4.,  5.,  6.,  7.],
          [ 8.,  9., 10., 11.],
          [12., 13., 14., 15.]],

         [[ 1.,  2.,  3.,  4.],
          [ 5.,  6.,  7.,  8.],
          [ 9., 10., 11., 12.],
          [13., 14., 15., 16.]]]])

如下所示，汇聚后输出通道的数量仍然是2

pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)

tensor([[[[ 5.,  7.],
          [13., 15.]],

         [[ 6.,  8.],
          [14., 16.]]]])

卷积神经网络（LeNet）

通过之前⼏节，我们学习了构建⼀个完整卷积神经⽹络的所需组件。回想⼀下，之前我们将softmax回归模型和多层感知机模型应⽤于Fashion-MNIST数据集中的服装图⽚。为了能够应⽤softmax回归
和多层感知机，我们⾸先将每个⼤⼩为28 × 28的图像展平为⼀个784维的固定⻓度的⼀维向量，然后⽤全连接层对其进⾏处理。⽽现在，我们已经掌握了卷积层的处理⽅法，我们可以在图像中保留空间结构。同时，⽤卷积层代替全连接层的另⼀个好处是：模型更简洁、所需的参数更少。

LeNet，它是最早发布的卷积神经⽹络之⼀，因其在计算机视觉任务中的⾼效性能⽽受到⼴泛关注。这了模型是由$AT\&T$贝尔实验室的研究员$Yann LeCun$在1989年提出的（并以其命名），目的是识别图像中的手写数字。

当时，LeNet取得了与SVM性能相媲美的成果，成为监督学习的主流方法。

总体来看，LeNet（LeNet-5）由两个部分组成：

• 卷积编码器：由两个卷积层组成
• 全连接层密集块：由三个全连接层组成

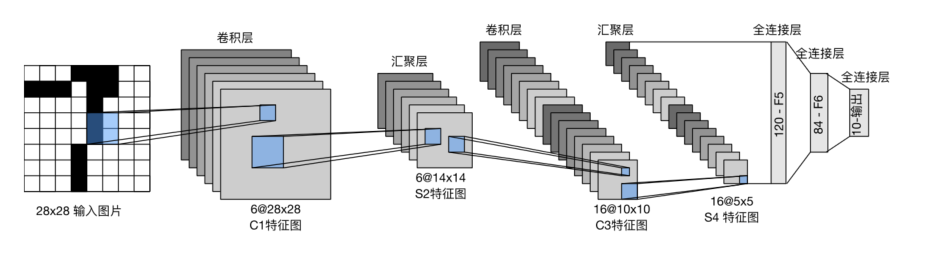
每个卷积块中的基本单元是⼀个卷积层、⼀个sigmoid激活函数和平均汇聚层。

虽然ReLU和最⼤汇聚层更有效，但它们在20世纪90年代还没有出现。

每个卷积层使⽤5 × 5卷积核和⼀个sigmoid激活函数。这些层将输⼊映射到多个⼆维特征输出，通常同时增加通道的数量。第⼀卷积层有6个输出通道，⽽第⼆个卷积层有16个输出通道。每个2 × 2池操作（步骤2）通过空间下采样将维数减少4倍。卷积的输出形状由批量⼤⼩、通道数、⾼度、宽度决定。

为了将卷积块的输出传递给稠密块，我们必须在⼩批量中展平每个样本。换⾔之，我们将这个四维输⼊转换成全连接层所期望的⼆维输⼊。这⾥的⼆维表⽰的第⼀个维度索引⼩批量中的样本，第⼆个维度给出每个样本的平⾯向量表⽰。LeNet的稠密块有三个全连接层，分别有120、84和10个输出。因为我们在执⾏分类任务，所以输出层的10维对应于最后输出结果的数量。

模型搭建

import torch
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(
                    nn.Conv2d(1, 6, kernel_size=5, padding=2),
                    nn.Sigmoid(),
                    nn.AvgPool2d(kernel_size=2, stride=2),
                    nn.Conv2d(6, 16, kernel_size=5),
                    nn.Sigmoid(),
                    nn.AvgPool2d(kernel_size=2, stride=2),
                    nn.Flatten(),
                    nn.Linear(16 * 5 * 5, 120),
                    nn.Sigmoid(),
                    nn.Linear(120, 84),
                    nn.Sigmoid(),
                    nn.Linear(84, 10))

我们对原始模型做了⼀点⼩改动，去掉了最后⼀层的⾼斯激活。

打印每层形状

X = torch.rand(size=(1, 1, 28, 28), dtype=torch.float32)
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__, 'output shape: \t', X.shape)

Conv2d output shape:      torch.Size([1, 6, 28, 28])
Sigmoid output shape:      torch.Size([1, 6, 28, 28])
AvgPool2d output shape:      torch.Size([1, 6, 14, 14])
Conv2d output shape:      torch.Size([1, 16, 10, 10])
Sigmoid output shape:      torch.Size([1, 16, 10, 10])
AvgPool2d output shape:      torch.Size([1, 16, 5, 5])
Flatten output shape:      torch.Size([1, 400])
Linear output shape:      torch.Size([1, 120])
Sigmoid output shape:      torch.Size([1, 120])
Linear output shape:      torch.Size([1, 84])
Sigmoid output shape:      torch.Size([1, 84])
Linear output shape:      torch.Size([1, 10])

模型训练

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)

为了进⾏评估，我们需要对evaluate_accuracy函数进⾏轻微的修改。由于完整的数据集位于内存中，因此在模型使⽤GPU计算数据集之前，我们需要将其复制到显存中。

def evaluate_accuracy_gpu(net, data_iter, device=None): #@save
    """使⽤GPU计算模型在数据集上的精度"""
    if isinstance(net, nn.Module):
        net.eval() # 设置为评估模式
        if not device:
            device = next(iter(net.parameters())).device
    # 正确预测的数量，总预测的数量
    metric = d2l.Accumulator(2)
    with torch.no_grad():
        for X, y in data_iter:
            if isinstance(X, list):
                # BERT微调所需的（之后将介绍）
                X = [x.to(device) for x in X]
            else:
                X = X.to(device)
            y = y.to(device)
            metric.add(d2l.accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]

为了使⽤GPU，我们还需要⼀点⼩改动。与train_epoch_ch3不同，在进⾏正向和反向传播之前，我们需要将每⼀⼩批量数据移动到我们指定的设备（例如GPU）上。

#@save
def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
    """⽤GPU训练模型(在第六章定义)"""
    def init_weights(m):
        if type(m) == nn.Linear or type(m) == nn.Conv2d:
            nn.init.xavier_uniform_(m.weight)  # 使用xavier进行参数的初始化
    net.apply(init_weights)
    print('training on', device)
    net.to(device)  # 将模型放入GPU
    optimizer = torch.optim.SGD(net.parameters(), lr=lr)
    loss = nn.CrossEntropyLoss()
    animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
                            legend=['train loss', 'train acc', 'test acc'])
    timer, num_batches = d2l.Timer(), len(train_iter)
    for epoch in range(num_epochs):
        # 训练损失之和，训练准确率之和，样本数
        metric = d2l.Accumulator(3)
        net.train()
        for i, (X, y) in enumerate(train_iter):
            timer.start()
            optimizer.zero_grad()  # 优化器梯度初始化
            X, y = X.to(device), y.to(device)  # 将数据放入GPU
            y_hat = net(X)  # 前向计算
            l = loss(y_hat, y)  # 计算损失
            l.backward()  # 反向传播，计算梯度
            optimizer.step()  # 利用梯度更新参数
            with torch.no_grad():
                metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
            timer.stop()
            train_l = metric[0] / metric[2]
            train_acc = metric[1] / metric[2]
            if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
                animator.add(epoch + (i + 1) / num_batches,
                            (train_l, train_acc, None))
        test_acc = evaluate_accuracy_gpu(net, test_iter)
        animator.add(epoch + 1, (None, None, test_acc))
    print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
          f'test acc {test_acc:.3f}')
    print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
          f'on {str(device)}')

lr, num_epochs = 0.9, 10
train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.458, train acc 0.828, test acc 0.808
41692.4 examples/sec on cuda:0