Ming-Log's Blog

记录生活中的点点滴滴

0%

Python数据科学_10_神经网络基础

发表于 更新于 分类于
本文字数： 27k 阅读时长 ≈ 25 分钟

手动推导人工神经网络

读取数据

1
2
import pandas as pd
import numpy as np
1
2
train_data = pd.read_csv('BPdata_tr.txt').values
test_data = pd.read_csv('BPdata_te.txt').values
1
2
print('训练数据尺寸：', train_data.shape)
print('测试数据尺寸：', test_data.shape)
训练数据尺寸： (500, 3)
测试数据尺寸： (100, 3)

数据集下载

1
2
3
4
5
6
# 将特征和标签分离
x_train = train_data[:, :-1]
y_train = train_data[:, -1:]

x_test = test_data[:, :-1]
y_test = test_data[:, -1:]

搭建神经网络模型

确定网络结构

1
2
3
4
5
6
7
8
9
10
# 数据一旦确定下来
# 网络的输入层和输出层的神经元数量就固定下来了
input_num = x_train.shape[1]
hidden_num =  4
output_num = y_train.shape[1]

print('神经网络结构：')
print('输入层神经元数量：', input_num)
print('隐藏层神经元数量：', hidden_num)
print('输出层神经元数量：', output_num)
神经网络结构：
输入层神经元数量： 2
隐藏层神经元数量： 4
输出层神经元数量： 1

根据网络结构进行参数初始化

1
2
3
4
V = np.random.random(size=(input_num, hidden_num))
P = np.random.random(size=(hidden_num, ))
W = np.random.random(size=(hidden_num, output_num))
Q = np.random.random(size=(output_num, ))
1
2
3
4
# 取出一个样本作为演示
x = x_train[0]
y = y_train[0]
x, y
(array([0.06573519, 0.044223  ]), array([0.00627679]))

1
V
array([[0.20544742, 0.31323623, 0.12468819, 0.98617925],
       [0.59215012, 0.23296201, 0.2592442 , 0.4892255 ]])

前向计算(forward)

1
2
def sigmoid(x):
    return 1/(1 + np.exp(-x))
1
2
def mse(y_true, y_pred):
    return 1/2 * np.sum((y_true - y_pred) ** 2)
1
2
3
4
5
6
7
8
9
10
# 隐藏层神经元的输入值
alpha = x@V - P
# 隐藏层神经元的输出值
b = sigmoid(alpha)
# 输出层神经元的输入值
beta = b@W - Q
# 输出层神经元的输出值
y_hat = sigmoid(beta)
# 计算误差
mse(y, y_hat)
0.17710730120764062

反向传播(backward)

1
2
3
4
5
# 定义存储梯度的数组容器
dV = np.zeros_like(V)
dP = np.zeros_like(P)
dW = np.zeros_like(W)
dQ = np.zeros_like(Q)
1
2
3
4
for j in range(output_num):
    for h in range(hidden_num):
        dW[h, j] = (y_hat[j] - y[j]) * y_hat[j] * (1 - y_hat[j]) * b[h]
    dQ[j] = (y_hat[j] - y[j]) * y_hat[j] * (1 - y_hat[j]) * (-1)
1
2
3
4
5
for j in range(output_num):
    for h in range(hidden_num):
        for i in range(input_num):
            dV[i, h] = (y_hat[j] - y[j]) * y_hat[j] * (1 - y_hat[j]) *  W[h, j] * b[h] * (1 - b[h]) * x[i]
        dP[h] = (y_hat[j] - y[j]) * y_hat[j] * (1 - y_hat[j]) *  W[h, j] * b[h] * (1 - b[h]) * (-1)

利用负梯度方向对参数值进行更新

1
2
yita = 1  # 步长，学习率
print('步长：', yita)
步长： 1

1
2
3
4
W = W - yita * dW
Q = Q - yita * dQ
V = V - yita * dV
P = P - yita * dP

循环选取每个样本对参数进行一次更新，并迭代多轮

1
2
epochs = 100  # 最大迭代次数
print('最大迭代次数：', epochs)
最大迭代次数： 100

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
Error = []  # 存储每轮迭代的平均误差
for epoch in range(epochs):
    E = []  # 存储每轮迭代过程中所有的样本误差
    for i in range(len(x_train)):
        # 取出一个样本作为演示
        x = x_train[i]
        y = y_train[i]
        # forward前向计算
        # 隐藏层神经元的输入值
        alpha = x@V - P
        # 隐藏层神经元的输出值
        b = sigmoid(alpha)
        # 输出层神经元的输入值
        beta = b@W - Q
        # 输出层神经元的输出值
        y_hat = sigmoid(beta)
        # 计算误差
        error = mse(y, y_hat)
        E.append(error)

        # 反向传播
        for j in range(output_num):
            for h in range(hidden_num):
                dW[h, j] = (y_hat[j] - y[j]) * y_hat[j] * (1 - y_hat[j]) * b[h]
            dQ[j] = (y_hat[j] - y[j]) * y_hat[j] * (1 - y_hat[j]) * (-1)

        for j in range(output_num):
            for h in range(hidden_num):
                for i in range(input_num):
                    dV[i, h] = (y_hat[j] - y[j]) * y_hat[j] * (1 - y_hat[j]) *  W[h, j] * b[h] * (1 - b[h]) * x[i]
                dP[h] = (y_hat[j] - y[j]) * y_hat[j] * (1 - y_hat[j]) *  W[h, j] * b[h] * (1 - b[h]) * (-1)

        # 利用梯度对参数进行更新
        W = W - yita * dW
        Q = Q - yita * dQ
        V = V - yita * dV
        P = P - yita * dP
    Error.append(np.mean(E))
    print(f'epoch: {epoch}  error: {np.mean(E)}')
epoch: 0  error: 0.0011830046453386962
epoch: 1  error: 0.0011830448558101821
epoch: 2  error: 0.0011823478474152882
epoch: 3  error: 0.0011816605089582175
epoch: 4  error: 0.001180978828304739
epoch: 5  error: 0.0011803032529185383
epoch: 6  error: 0.0011796343625671642
epoch: 7  error: 0.001178972358562127
epoch: 8  error: 0.001178317156957608
epoch: 9  error: 0.0011776685094095774
epoch: 10  error: 0.0011770260789136123
epoch: 11  error: 0.0011763894802793752
epoch: 12  error: 0.00117575830031352
epoch: 13  error: 0.0011751321073427104
epoch: 14  error: 0.0011745104553182975
epoch: 15  error: 0.0011738928851878425
epoch: 16  error: 0.0011732789248728255
epoch: 17  error: 0.00117266808851052
epoch: 18  error: 0.001172059875278599
epoch: 19  error: 0.0011714537679528188
epoch: 20  error: 0.0011708492312647487
epoch: 21  error: 0.0011702457100847769
epoch: 22  error: 0.0011696426274343938
epoch: 23  error: 0.0011690393823204199
epoch: 24  error: 0.001168435347377338
epoch: 25  error: 0.001167829866299602
epoch: 26  error: 0.0011672222510424142
epoch: 27  error: 0.0011666117787665015
epoch: 28  error: 0.001165997688499305
epoch: 29  error: 0.0011653791774817975
epoch: 30  error: 0.0011647553971665082
epoch: 31  error: 0.0011641254488284009
epoch: 32  error: 0.0011634883787457406
epoch: 33  error: 0.0011628431729030768
epoch: 34  error: 0.0011621887511628595
epoch: 35  error: 0.0011615239608458111
epoch: 36  error: 0.0011608475696531036
epoch: 37  error: 0.0011601582578553175
epoch: 38  error: 0.0011594546096642079
epoch: 39  error: 0.0011587351036931284
epoch: 40  error: 0.001157998102400633
epoch: 41  error: 0.0011572418403990152
epoch: 42  error: 0.0011564644114952479
epoch: 43  error: 0.0011556637543157923
epoch: 44  error: 0.001154837636348849
epoch: 45  error: 0.001153983636217666
epoch: 46  error: 0.0011530991239762749
epoch: 47  error: 0.0011521812391943529
epoch: 48  error: 0.0011512268665705323
epoch: 49  error: 0.0011502326087833741
epoch: 50  error: 0.0011491947562560782
epoch: 51  error: 0.0011481092534749123
epoch: 52  error: 0.0011469716614621555
epoch: 53  error: 0.0011457771159623469
epoch: 54  error: 0.0011445202808558692
epoch: 55  error: 0.001143195296267188
epoch: 56  error: 0.0011417957207868832
epoch: 57  error: 0.0011403144671784764
epoch: 58  error: 0.0011387437308945088
epoch: 59  error: 0.0011370749106839142
epoch: 60  error: 0.0011352985205377534
epoch: 61  error: 0.0011334040921972895
epoch: 62  error: 0.001131380067443013
epoch: 63  error: 0.0011292136794032966
epoch: 64  error: 0.001126890822176482
epoch: 65  error: 0.0011243959081628908
epoch: 66  error: 0.0011217117126688509
epoch: 67  error: 0.0011188192055924693
epoch: 68  error: 0.001115697370353711
epoch: 69  error: 0.0011123230107171166
epoch: 70  error: 0.0011086705468067862
epoch: 71  error: 0.0011047118024676002
epoch: 72  error: 0.0011004157872258951
epoch: 73  error: 0.0010957484774922336
epoch: 74  error: 0.0010906726033748958
epoch: 75  error: 0.0010851474495792693
epoch: 76  error: 0.0010791286813915733
epoch: 77  error: 0.0010725682097055716
epoch: 78  error: 0.0010654141124414116
epoch: 79  error: 0.0010576106334783612
epoch: 80  error: 0.001049098284269502
epoch: 81  error: 0.0010398140774362749
epoch: 82  error: 0.0010296919255574344
epoch: 83  error: 0.0010186632416443278
epoch: 84  error: 0.001006657779858423
epoch: 85  error: 0.0009936047551503473
epoch: 86  error: 0.0009794342778181161
epoch: 87  error: 0.000964079132541856
epoch: 88  error: 0.0009474769202972912
epoch: 89  error: 0.0009295725648519173
epoch: 90  error: 0.0009103211627702767
epoch: 91  error: 0.0008896911269390674
epoch: 92  error: 0.0008676675391628334
epoch: 93  error: 0.0008442555887644414
epoch: 94  error: 0.0008194839336178838
epoch: 95  error: 0.0007934077808193434
epoch: 96  error: 0.0007661114503347067
epoch: 97  error: 0.00073771016136203
epoch: 98  error: 0.0007083507734585452
epoch: 99  error: 0.0006782112287891603

利用训练好的参数去预测测试数据

1
2
3
4
5
6
7
8
9
x = x_test
# 隐藏层神经元的输入值
alpha = x@V - P
# 隐藏层神经元的输出值
b = sigmoid(alpha)
# 输出层神经元的输入值
beta = b@W - Q
# 输出层神经元的输出值
y_hat = sigmoid(beta)

打包为函数

1
2
import pandas as pd
import numpy as np
1
2
3
4
5
6
7
# 非线性激活函数
def sigmoid(x):
    return 1/(1 + np.exp(-x))

# 损失函数
def mse(y_true, y_pred):
    return 1/2 * np.sum((y_true - y_pred) ** 2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
def BP_network(x_trian, y_train, hidden_num=4, yita=0.5, epochs=100):
    # 数据一旦确定下来
    # 网络的输入层和输出层的神经元数量就固定下来了
    input_num = x_train.shape[1]
    output_num = y_train.shape[1]
    
    V = np.random.random(size=(input_num, hidden_num))
    P = np.random.random(size=(hidden_num, ))
    W = np.random.random(size=(hidden_num, output_num))
    Q = np.random.random(size=(output_num, ))
    
    # 定义存储梯度的数组容器
    dV = np.zeros_like(V)
    dP = np.zeros_like(P)
    dW = np.zeros_like(W)
    dQ = np.zeros_like(Q)
    
    Error = []  # 存储每轮迭代的平均误差
    for epoch in range(epochs):
        E = []  # 存储每轮迭代过程中所有的样本误差
        for i in range(len(x_train)):
            # 取出一个样本作为演示
            x = x_train[i]
            y = y_train[i]
            # forward前向计算
            # 隐藏层神经元的输入值
            alpha = x@V - P
            # 隐藏层神经元的输出值
            b = sigmoid(alpha)
            # 输出层神经元的输入值
            beta = b@W - Q
            # 输出层神经元的输出值
            y_hat = sigmoid(beta)
            # 计算误差
            error = mse(y, y_hat)
            E.append(error)

            # 反向传播
            for j in range(output_num):
                for h in range(hidden_num):
                    dW[h, j] = (y_hat[j] - y[j]) * y_hat[j] * (1 - y_hat[j]) * b[h]
                dQ[j] = (y_hat[j] - y[j]) * y_hat[j] * (1 - y_hat[j]) * (-1)

            for j in range(output_num):
                for h in range(hidden_num):
                    for i in range(input_num):
                        dV[i, h] = (y_hat[j] - y[j]) * y_hat[j] * (1 - y_hat[j]) *  W[h, j] * b[h] * (1 - b[h]) * x[i]
                    dP[h] = (y_hat[j] - y[j]) * y_hat[j] * (1 - y_hat[j]) *  W[h, j] * b[h] * (1 - b[h]) * (-1)

            # 利用梯度对参数进行更新
            W = W - yita * dW
            Q = Q - yita * dQ
            V = V - yita * dV
            P = P - yita * dP
        Error.append(np.mean(E))
        print(f'epoch: {epoch}  error: {np.mean(E)}')
    params = {}
    params['W'] = W
    params['Q'] = Q
    params['V'] = V
    params['P'] = P
    return params
1
2
train_data = pd.read_csv('BPdata_tr.txt').values
test_data = pd.read_csv('BPdata_te.txt').values
1
2
3
4
5
6
# 将特征和标签分离
x_train = train_data[:, :-1]
y_train = train_data[:, -1:]

x_test = test_data[:, :-1]
y_test = test_data[:, -1:]
1
params = BP_network(x_train, y_train )
epoch: 0  error: 0.021497283338905878
epoch: 1  error: 0.018216032153659224
epoch: 2  error: 0.01479201956709213
epoch: 3  error: 0.01057914963442369
epoch: 4  error: 0.006753025325782918
epoch: 5  error: 0.004139570123532772
epoch: 6  error: 0.0026627979059380687
epoch: 7  error: 0.001901516497840612
epoch: 8  error: 0.001521294464862305
epoch: 9  error: 0.001332153306805115
epoch: 10  error: 0.0012374384249401386
epoch: 11  error: 0.001189509134283564
epoch: 12  error: 0.0011649487572739788
epoch: 13  error: 0.0011521669622316137
epoch: 14  error: 0.001145373218750827
epoch: 15  error: 0.001141648229167907
epoch: 16  error: 0.0011395082616882544
epoch: 17  error: 0.0011381937603494887
epoch: 18  error: 0.0011373132841759395
epoch: 19  error: 0.0011366637525846647
epoch: 20  error: 0.0011361390434147722
epoch: 21  error: 0.0011356832339605076
epoch: 22  error: 0.0011352665517595849
epoch: 23  error: 0.0011348729423759601
epoch: 24  error: 0.0011344936085169839
epoch: 25  error: 0.0011341236323305695
epoch: 26  error: 0.0011337601969279706
epoch: 27  error: 0.0011334016416309491
epoch: 28  error: 0.001133046954492023
epoch: 29  error: 0.001132695495877507
epoch: 30  error: 0.00113234684530785
epoch: 31  error: 0.0011320007148392904
epoch: 32  error: 0.0011316568989093647
epoch: 33  error: 0.0011313152445320196
epoch: 34  error: 0.0011309756330966038
epoch: 35  error: 0.001130637968947203
epoch: 36  error: 0.0011303021720297953
epoch: 37  error: 0.0011299681730469137
epoch: 38  error: 0.001129635910199322
epoch: 39  error: 0.0011293053269569495
epoch: 40  error: 0.0011289763705118413
epoch: 41  error: 0.0011286489906913299
epoch: 42  error: 0.0011283231391863602
epoch: 43  error: 0.0011279987689981823
epoch: 44  error: 0.0011276758340377168
epoch: 45  error: 0.0011273542888323531
epoch: 46  error: 0.0011270340883087683
epoch: 47  error: 0.0011267151876296882
epoch: 48  error: 0.0011263975420690308
epoch: 49  error: 0.0011260811069143991
epoch: 50  error: 0.001125765837389043
epoch: 51  error: 0.0011254516885876864
epoch: 52  error: 0.0011251386154221934
epoch: 53  error: 0.0011248265725741923
epoch: 54  error: 0.0011245155144525634
epoch: 55  error: 0.0011242053951543067
epoch: 56  error: 0.0011238961684276892
epoch: 57  error: 0.0011235877876368857
epoch: 58  error: 0.0011232802057275211
epoch: 59  error: 0.0011229733751927117
epoch: 60  error: 0.0011226672480392419
epoch: 61  error: 0.0011223617757536793
epoch: 62  error: 0.0011220569092681976
epoch: 63  error: 0.0011217525989259966
epoch: 64  error: 0.0011214487944461646
epoch: 65  error: 0.0011211454448879145
epoch: 66  error: 0.0011208424986140725
epoch: 67  error: 0.0011205399032537802
epoch: 68  error: 0.0011202376056643044
epoch: 69  error: 0.0011199355518919138
epoch: 70  error: 0.0011196336871317461
epoch: 71  error: 0.0011193319556866035
epoch: 72  error: 0.001119030300924626
epoch: 73  error: 0.0011187286652357656
epoch: 74  error: 0.001118426989987011
epoch: 75  error: 0.001118125215476297
epoch: 76  error: 0.0011178232808850234
epoch: 77  error: 0.0011175211242291357
epoch: 78  error: 0.0011172186823086897
epoch: 79  error: 0.00111691589065582
epoch: 80  error: 0.001116612683481063
epoch: 81  error: 0.0011163089936179356
epoch: 82  error: 0.0011160047524657122
epoch: 83  error: 0.0011156998899303063
epoch: 84  error: 0.0011153943343631795
epoch: 85  error: 0.0011150880124981958
epoch: 86  error: 0.0011147808493863192
epoch: 87  error: 0.0011144727683280796
epoch: 88  error: 0.001114163690803701
epoch: 89  error: 0.0011138535364007848
epoch: 90  error: 0.0011135422227394694
epoch: 91  error: 0.001113229665394928
epoch: 92  error: 0.001112915777817123
epoch: 93  error: 0.0011126004712476724
epoch: 94  error: 0.0011122836546337337
epoch: 95  error: 0.0011119652345387616
epoch: 96  error: 0.0011116451150500178
epoch: 97  error: 0.001111323197682695
epoch: 98  error: 0.0011109993812805196
epoch: 99  error: 0.001110673561912669

1
params
{'W': array([[1.27743155],
        [1.73038355],
        [3.22378892],
        [2.45123304]]),
 'Q': array([4.65009782]),
 'V': array([[1.69795705, 1.58954355, 1.94205688, 1.55196131],
        [0.62734663, 1.37065212, 2.08648462, 2.01140756]]),
 'P': array([1.19343114, 1.20736236, 1.7276384 , 1.5529578 ])}

1
2
3
4
5
6
7
8
9
10
x = x_test
alpha = x@params['V'] - params['P']
# 隐藏层神经元的输出值
b = sigmoid(alpha)
# 输出层神经元的输入值
beta = b@params['W'] - params['Q']
# 输出层神经元的输出值
y_hat = sigmoid(beta)
# 计算误差
error = mse(y_test, y_hat)
1
error
0.15861277069749924

调用自写的模块

1
from BP_net import BPnet
1
self_BP = BPnet(verbose=1)
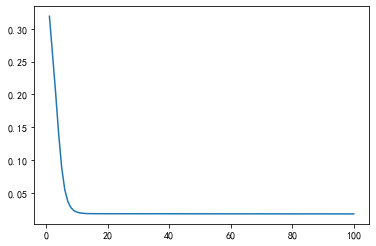
1
self_BP.fit(x_train, y_train)
Data Num: 500
Epoch:1, 100%[===============================>]0.01s, loss=0.3232906774
Epoch:2, 100%[===============================>]0.01s, loss=0.2648733180
Epoch:3, 100%[===============================>]0.02s, loss=0.1992836122
Epoch:4, 100%[===============================>]0.01s, loss=0.1308549527
Epoch:5, 100%[===============================>]0.01s, loss=0.0787782641
Epoch:6, 100%[===============================>]0.01s, loss=0.0480898869
Epoch:7, 100%[===============================>]0.01s, loss=0.0324464792
Epoch:8, 100%[===============================>]0.01s, loss=0.0249232800
Epoch:9, 100%[===============================>]0.01s, loss=0.0213602957
Epoch:10, 100%[===============================>]0.01s, loss=0.0196731016
Epoch:11, 100%[===============================>]0.01s, loss=0.0188717199
Epoch:12, 100%[===============================>]0.01s, loss=0.0184901873
Epoch:13, 100%[===============================>]0.01s, loss=0.0183081722
Epoch:14, 100%[===============================>]0.01s, loss=0.0182208020
Epoch:15, 100%[===============================>]0.01s, loss=0.0181779524
Epoch:16, 100%[===============================>]0.01s, loss=0.0181556725
Epoch:17, 100%[===============================>]0.01s, loss=0.0181425884
Epoch:18, 100%[===============================>]0.01s, loss=0.0181333754
Epoch:19, 100%[===============================>]0.01s, loss=0.0181256064
Epoch:20, 100%[===============================>]0.01s, loss=0.0181182272
Epoch:21, 100%[===============================>]0.01s, loss=0.0181108211
Epoch:22, 100%[===============================>]0.01s, loss=0.0181032573
Epoch:23, 100%[===============================>]0.01s, loss=0.0180955246
Epoch:24, 100%[===============================>]0.01s, loss=0.0180876552
Epoch:25, 100%[===============================>]0.01s, loss=0.0180796917
Epoch:26, 100%[===============================>]0.01s, loss=0.0180716738
Epoch:27, 100%[===============================>]0.01s, loss=0.0180636339
Epoch:28, 100%[===============================>]0.01s, loss=0.0180555965
Epoch:29, 100%[===============================>]0.01s, loss=0.0180475795
Epoch:30, 100%[===============================>]0.01s, loss=0.0180395956
Epoch:31, 100%[===============================>]0.01s, loss=0.0180316531
Epoch:32, 100%[===============================>]0.01s, loss=0.0180237573
Epoch:33, 100%[===============================>]0.01s, loss=0.0180159114
Epoch:34, 100%[===============================>]0.01s, loss=0.0180081169
Epoch:35, 100%[===============================>]0.01s, loss=0.0180003742
Epoch:36, 100%[===============================>]0.02s, loss=0.0179926829
Epoch:37, 100%[===============================>]0.01s, loss=0.0179850419
Epoch:38, 100%[===============================>]0.01s, loss=0.0179774501
Epoch:39, 100%[===============================>]0.01s, loss=0.0179699057
Epoch:40, 100%[===============================>]0.01s, loss=0.0179624069
Epoch:41, 100%[===============================>]0.01s, loss=0.0179549519
Epoch:42, 100%[===============================>]0.01s, loss=0.0179475386
Epoch:43, 100%[===============================>]0.01s, loss=0.0179401651
Epoch:44, 100%[===============================>]0.01s, loss=0.0179328291
Epoch:45, 100%[===============================>]0.01s, loss=0.0179255286
Epoch:46, 100%[===============================>]0.01s, loss=0.0179182616
Epoch:47, 100%[===============================>]0.01s, loss=0.0179110258
Epoch:48, 100%[===============================>]0.01s, loss=0.0179038191
Epoch:49, 100%[===============================>]0.01s, loss=0.0178966394
Epoch:50, 100%[===============================>]0.01s, loss=0.0178894845
Epoch:51, 100%[===============================>]0.02s, loss=0.0178823522
Epoch:52, 100%[===============================>]0.01s, loss=0.0178752404
Epoch:53, 100%[===============================>]0.01s, loss=0.0178681467
Epoch:54, 100%[===============================>]0.01s, loss=0.0178610691
Epoch:55, 100%[===============================>]0.01s, loss=0.0178540052
Epoch:56, 100%[===============================>]0.01s, loss=0.0178469527
Epoch:57, 100%[===============================>]0.01s, loss=0.0178399093
Epoch:58, 100%[===============================>]0.01s, loss=0.0178328726
Epoch:59, 100%[===============================>]0.01s, loss=0.0178258403
Epoch:60, 100%[===============================>]0.01s, loss=0.0178188099
Epoch:61, 100%[===============================>]0.01s, loss=0.0178117788
Epoch:62, 100%[===============================>]0.01s, loss=0.0178047446
Epoch:63, 100%[===============================>]0.01s, loss=0.0177977046
Epoch:64, 100%[===============================>]0.01s, loss=0.0177906562
Epoch:65, 100%[===============================>]0.01s, loss=0.0177835965
Epoch:66, 100%[===============================>]0.01s, loss=0.0177765229
Epoch:67, 100%[===============================>]0.02s, loss=0.0177694323
Epoch:68, 100%[===============================>]0.01s, loss=0.0177623220
Epoch:69, 100%[===============================>]0.01s, loss=0.0177551887
Epoch:70, 100%[===============================>]0.01s, loss=0.0177480293
Epoch:71, 100%[===============================>]0.01s, loss=0.0177408406
Epoch:72, 100%[===============================>]0.01s, loss=0.0177336193
Epoch:73, 100%[===============================>]0.01s, loss=0.0177263618
Epoch:74, 100%[===============================>]0.01s, loss=0.0177190646
Epoch:75, 100%[===============================>]0.01s, loss=0.0177117241
Epoch:76, 100%[===============================>]0.01s, loss=0.0177043363
Epoch:77, 100%[===============================>]0.01s, loss=0.0176968972
Epoch:78, 100%[===============================>]0.01s, loss=0.0176894029
Epoch:79, 100%[===============================>]0.01s, loss=0.0176818489
Epoch:80, 100%[===============================>]0.01s, loss=0.0176742309
Epoch:81, 100%[===============================>]0.01s, loss=0.0176665443
Epoch:82, 100%[===============================>]0.02s, loss=0.0176587842
Epoch:83, 100%[===============================>]0.01s, loss=0.0176509456
Epoch:84, 100%[===============================>]0.01s, loss=0.0176430234
Epoch:85, 100%[===============================>]0.01s, loss=0.0176350122
Epoch:86, 100%[===============================>]0.01s, loss=0.0176269064
Epoch:87, 100%[===============================>]0.01s, loss=0.0176187000
Epoch:88, 100%[===============================>]0.01s, loss=0.0176103869
Epoch:89, 100%[===============================>]0.01s, loss=0.0176019608
Epoch:90, 100%[===============================>]0.01s, loss=0.0175934149
Epoch:91, 100%[===============================>]0.01s, loss=0.0175847423
Epoch:92, 100%[===============================>]0.01s, loss=0.0175759358
Epoch:93, 100%[===============================>]0.01s, loss=0.0175669877
Epoch:94, 100%[===============================>]0.01s, loss=0.0175578900
Epoch:95, 100%[===============================>]0.01s, loss=0.0175486344
Epoch:96, 100%[===============================>]0.01s, loss=0.0175392121
Epoch:97, 100%[===============================>]0.01s, loss=0.0175296141
Epoch:98, 100%[===============================>]0.02s, loss=0.0175198308
Epoch:99, 100%[===============================>]0.01s, loss=0.0175098521
Epoch:100, 100%[===============================>]0.01s, loss=0.0174996675
Fit Success, Fit time:0.915087(s)

1
self_BP.plot_fit()

output_43_0_202303092114

保存模型训练参数

1
2
# 保存参数
self_BP.save_params('BP_params.json')
1
2
# 定义新模型然后导入已有的参数
self_BP2 = BPnet()
1
self_BP2.load_params('BP_params.json')
1
self_BP2.predict(x_test)[:5]
array([[0.49421352],
       [0.26958529],
       [0.10800705],
       [0.7978499 ],
       [0.64725221]])

保存整个模型

1
from core.models import save_model, load_model
1
save_model('models.pkl', self_BP)
1
model = load_model('models.pkl')
1
model.predict(x_test)[:5]
array([[0.49421352],
       [0.26958529],
       [0.10800705],
       [0.7978499 ],
       [0.64725221]])

调用Sklean中自带的神经网络模型

1
from sklearn.neural_network import MLPRegressor
1
2
3
4
5
6
7
8
# hidden_layer_sizes: 隐藏层神经元数量（结构）
# learning_rate_init: 学习率大小
# max_iter: 最大迭代次数
# verbose: 是否打印出训练过程
mlp_model = MLPRegressor(hidden_layer_sizes=10, 
                                                         learning_rate_init=0.01,
                                                         max_iter=200,
                                                         verbose=1)
1
mlp_model.fit(x_train, y_train)
Iteration 1, loss = 0.08260635
Iteration 2, loss = 0.06246179
Iteration 3, loss = 0.04580418
Iteration 4, loss = 0.03332414
Iteration 5, loss = 0.02396149
Iteration 6, loss = 0.01779838
Iteration 7, loss = 0.01429897
Iteration 8, loss = 0.01237406
Iteration 9, loss = 0.01179750
Iteration 10, loss = 0.01163056
Iteration 11, loss = 0.01161769
Iteration 12, loss = 0.01136085
Iteration 13, loss = 0.01082563
Iteration 14, loss = 0.01007022
Iteration 15, loss = 0.00923557
Iteration 16, loss = 0.00845418
Iteration 17, loss = 0.00781733
Iteration 18, loss = 0.00726607
Iteration 19, loss = 0.00683927
Iteration 20, loss = 0.00648799
Iteration 21, loss = 0.00612407
Iteration 22, loss = 0.00577429
Iteration 23, loss = 0.00538861
Iteration 24, loss = 0.00504740
Iteration 25, loss = 0.00470932
Iteration 26, loss = 0.00441425
Iteration 27, loss = 0.00414589
Iteration 28, loss = 0.00390004
Iteration 29, loss = 0.00366903
Iteration 30, loss = 0.00345395
Iteration 31, loss = 0.00324042
Iteration 32, loss = 0.00305015
Iteration 33, loss = 0.00287143
Iteration 34, loss = 0.00270487
Iteration 35, loss = 0.00255550
Iteration 36, loss = 0.00240999
Iteration 37, loss = 0.00228839
Iteration 38, loss = 0.00216483
Iteration 39, loss = 0.00205609
Iteration 40, loss = 0.00195486
Iteration 41, loss = 0.00186768
Iteration 42, loss = 0.00178074
Iteration 43, loss = 0.00170450
Iteration 44, loss = 0.00163618
Iteration 45, loss = 0.00157377
Iteration 46, loss = 0.00152096
Iteration 47, loss = 0.00146531
Iteration 48, loss = 0.00142252
Iteration 49, loss = 0.00137995
Iteration 50, loss = 0.00134062
Iteration 51, loss = 0.00131050
Training loss did not improve more than tol=0.000100 for 10 consecutive epochs. Stopping.

1
mlp_model.predict(x_test)[:5]
array([0.48890992, 0.30715008, 0.11244658, 0.75094736, 0.60382594])

自写神经网络代码

主类：BPnet

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
import numpy as np
import json
import matplotlib.pyplot as plt
from core.activation import sigmoid
from core.losses import se
import time

class BPnet:
    # 初始化函数
    def __init__(self,
                 hidden_num=4,
                 yita=0.5,
                 epochs=100,
                 verbose=0,
                 activation=sigmoid,
                 loss=se,
                 batch_size=16,
                 shuffer=True):
        self.hidden_num = hidden_num
        self.yita = yita
        self.epochs = epochs
        self.verbose = verbose
        self.activation = activation
        self.loss = loss
        self.batch_size = batch_size
        self.shuffer = shuffer
        self.params = {}
        self.E = []

    # 前向计算
    def forward(self, x):
        alpha = x @ self.params['v'] - self.params['P']
        b = sigmoid(alpha)
        beta = b @ self.params['w'] - self.params['Q']
        y_hat = sigmoid(beta)
        return y_hat, b

    # 梯度置零
    def gradient_zeros(self, d_params):
        res_params = {}
        for i, j in d_params.items():
            res_params[i] = np.zeros_like(j)
        return res_params

    # 模型训练
    def fit(self, x_train, y_train):
        # 数据量
        N = len(x_train)
        print('Data Num:', N)
        # 训练数据打乱
        if self.shuffer:
            index = np.arange(N)
            np.random.shuffle(index)
            x_train = x_train[index]
            y_train = y_train[index]
        start_time = time.time()
        input_num = x_train.shape[1]
        output_num = y_train.shape[1]
        # 初始化参数
        self.params['v'] = np.random.random((input_num, self.hidden_num))
        self.params['P'] = np.random.random(self.hidden_num)
        self.params['w'] = np.random.random((self.hidden_num, output_num))
        self.params['Q'] = np.random.random(output_num)
        # 初始化梯度矩阵
        d_params = self.params.copy()
        # 4. 开始迭代，训练参数
        for epoch in range(1, self.epochs + 1):
            Error = []
            # batch_size
            group_num = N // self.batch_size
            start = time.perf_counter()
            for n in range(group_num + 1):
                # 获取单个样本
                x = x_train[n*self.batch_size: (n+1) * self.batch_size]
                y = y_train[n*self.batch_size: (n+1) * self.batch_size]
                # 进行前向计算
                y_hat, b = self.forward(x)
                # print(b)
                # 计算误差
                error = self.loss(y, y_hat)
                Error.append(error)  # 将本轮所有样本的误差存储到列表
                # 梯度置零
                d_params = self.gradient_zeros(d_params)
                # 4. 计算梯度进行反向更新参数
                for j in range(output_num):
                    for h in range(self.hidden_num):
                        d_params['w'][h, j] = np.sum((y_hat[:, j] - y[:, j]) * y_hat[:, j] * \
                                    (1 - y_hat[:, j]) * b[:, h])
                    d_params['Q'][j] += np.sum((y_hat[:, j] - y[:, j]) * y_hat[:, j] * \
                             (1 - y_hat[:, j]) * (-1))
                for j in range(output_num):
                    for h in range(self.hidden_num):
                        for i in range(input_num):
                            d_params['v'][i, h] = np.sum((y_hat[:, j] - y[:, j]) * y_hat[:, j] * (1 - y_hat[:, j]) \
                                        * self.params['w'][h, j] * b[:, h] * (1 - b[:, h]) * x[:, i])
                        d_params['P'][h] = np.sum((y_hat[:, j] - y[:, j]) * y_hat[:, j] * (1 - y_hat[:, j]) \
                                 * self.params['w'][h, j] * b[:, h] * (1 - b[:, h]) * (-1))
                # 利用梯度进参数的更新
                self.params['w'] = self.params['w'] - self.yita * d_params['w']
                self.params['Q'] = self.params['Q'] - self.yita * d_params['Q']
                self.params['v'] = self.params['v'] - self.yita * d_params['v']
                self.params['P'] = self.params['P'] - self.yita * d_params['P']
                finsh = "=" * n
                need_do = " " * (group_num - n)
                dur = time.perf_counter() - start
                # 进度条
                if self.verbose == 1:
                    print("\rEpoch:{},{:4.0f}%[{}>{}]{:.2f}s, loss={:.10f}".format(epoch, n / group_num * 100, finsh, need_do,
                                                                                      dur, np.mean(Error)), end="")
            if self.verbose == 1:
                print()  # 每轮训练完毕后换行
            self.E.append(np.mean(Error))
        end_time = time.time()
        print('Fit Success, Fit time:%f(s)' % (end_time - start_time))

    # 模型预测
    def predict(self, x):
        return self.forward(x)[0]

    # 模型参数存储
    def save_params(self, file_path):
        tmp_dict = {i: j.tolist() for i, j in self.params.items()}
        with open(file_path, 'w') as f:
            json.dump(tmp_dict, f)

    # 模型参数加载
    def load_params(self, file_path):
        with open(file_path, 'r') as f:
            self.params = json.load(f)

    # 模型训练过程绘制
    def plot_fit(self, title=None, xlabel=None, ylabel=None, save_fig=None):
        # 设置中文正常显示
        plt.rcParams['font.sans-serif'] = ['SimHei']
        plt.rcParams['axes.unicode_minus'] = False
        plt.plot(range(1, self.epochs+1), self.E)
        plt.title(title)
        plt.xlabel(xlabel)
        plt.ylabel(ylabel)
        if save_fig:
            plt.savefig(save_fig)
        plt.show()

core模块内容：

主要包含4个脚本

image-20220907112849746

activation.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# -*- coding: utf-8 -*-
"""
@Time:2022/7/11 19:17
@Author:Ming-Log
@File:activation.py
@IDE:PyCharm
"""
import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def relu(x):
    x[x > 0] = 0
    return x

def softmax(x):
    return np.exp(x) / np.sum(np.exp(x))

def log_softmax(x):
    return np.log(np.exp(x) / np.sum(np.exp(x)))

losses.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# -*- coding: utf-8 -*-
"""
@Time:2022/7/11 19:17
@Author:Ming-Log
@File:losses.py
@IDE:PyCharm
"""
import numpy as np

def se(y_true, y_pred):
    return 1/2 * np.sum(np.square(y_pred - y_true))

def mse(y_true, y_pred):
    return np.mean(np.square(y_pred - y_true))

metrics.py

1
2
3
4
5
6
7
8
import numpy as np


def se(y_true, y_pred):
    return 1/2 * np.sum(np.square(y_pred - y_true))

def mse(y_true, y_pred):
    return np.mean(np.square(y_pred - y_true))

models.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# -*- coding: utf-8 -*-
"""
@Time:2022/7/13 16:33
@Author:Ming-Log
@File:models.py
@IDE:PyCharm
"""
import pickle

def save_model(file_path, model):
    with open(file_path, 'wb') as f:
        pickle.dump(model, f)

def load_model(file_path):
    with open(file_path, 'rb') as f:
        model = pickle.load(f)
    return model

-------------本文结束感谢您的阅读-------------