Ming-Log's Blog

记录生活中的点点滴滴

0%

隐马尔可夫模型(HMM)及其应用

发表于 更新于 分类于
本文字数： 8.3k 阅读时长 ≈ 8 分钟

马尔可夫模型

首先，我们来看一下马尔可夫模型。

马尔可夫模型（Markov Model）：马尔可夫模型是一种统计模型，它基于马尔可夫性质进行建模。马尔可夫性质指的是系统的下一个状态仅取决于其当前状态，而与过去的状态无关。这种性质使得马尔可夫模型在处理一系列具有时间依赖性的数据时非常有用。

广泛应用在语音识别，词性自动标注，音字转换，概率文法等各个自然语言处理等应用领域。经过长期发展，尤其是在语音识别中的成功应用，使它成为一种通用的统计工具。

举个具体的例子。例如：天气变化种类{晴天，多云，雷雨}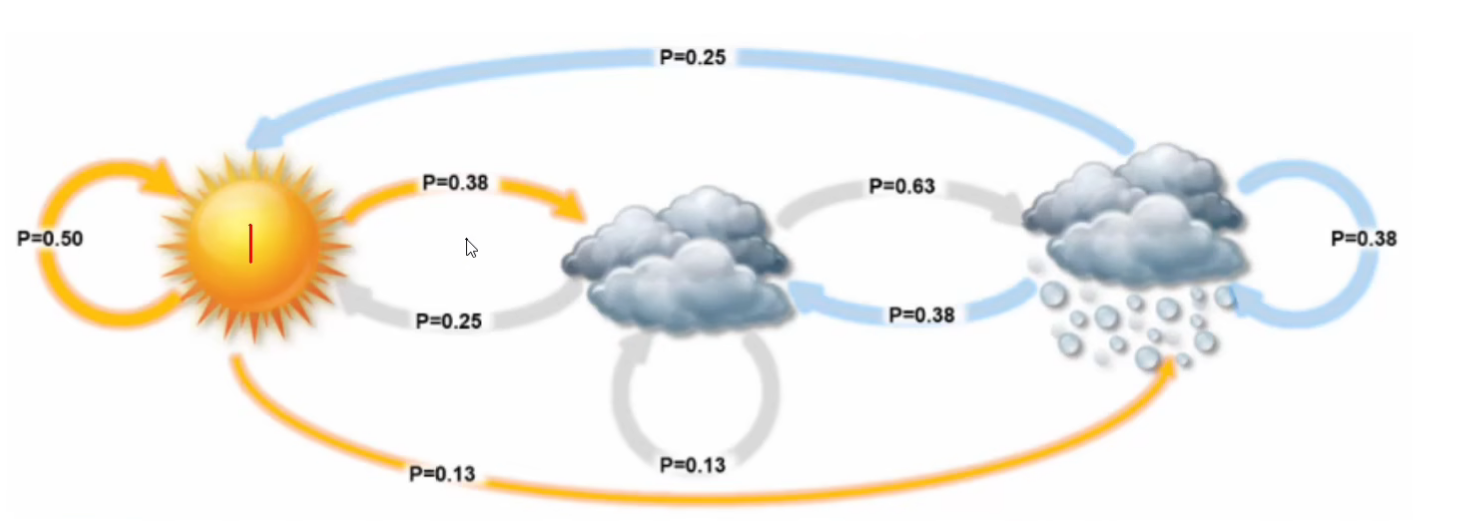
image-20240325195611737

状态转移矩阵：

有了状态转移矩阵那么，我们只需要知道今天的天气情况就可以推导出以后天气的情况。

今天的天气情况我们称为初始概率，如果是晴天那么初始概率为:

image-20240325195917236

那么我们就可以计算出明天的天气情况为：

所以明天天晴的概率为0.5, 多云的概率为0.25, 下雨的概率为0.25

以此类推，继续求出后天天气的概率

这个就是马尔可夫模型，给定初始状态和不同状态之间的转移矩阵即可求出后续任意时间的状态概率分布。

1
import numpy as np
1
2
3
4
5
6
7
# 定义转移概率矩阵
W = np.array([[0.5, 0.375, 0.125],
         [0.25, 0.25, 0.5],
         [0.25, 0.375, 0.375]])

# 定义初始概率矩阵
a_0 = np.array([1.0, 0.0, 0.0])
1
2
3
# 时刻1（明天）的天气情况
a_1 = a_0@W.T
a_1
array([0.5 , 0.25, 0.25])

1
2
3
# 时刻2（后天）的天气情况
a_2 = a_1@W.T
a_2
array([0.375 , 0.3125, 0.3125])

隐马尔可夫模型（HMM）

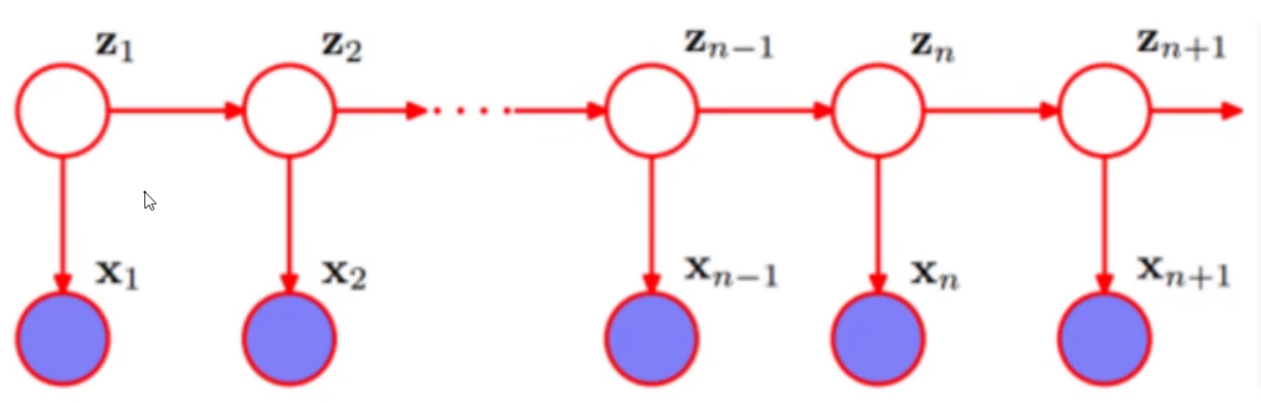
隐马尔可夫模型（Hidden Markov Model），是一种统计模型，用于预测一系列隐藏状态的概率，这些隐藏状态是基于给定的观察状态得出的。在HMM中，状态具有时序关系，每个时刻处于某一状态，所取得的观测值与状态相关。

HMM基于两个基本假设：

  1. 当前的状态只和前一状态有关
  2. 某个观测只和生成它的状态有关。

HMM广泛应用于数据科学和机器学习任务中，包括但不限于语音识别、图像分割、股市预测以及生物信息学等领域。在语音识别中，HMM被用于对语音信号的声学特征进行建模，以便识别单词和短语。在图像分割中，HMM则用于识别图像中的对象，通过分析形状、颜色和纹理等特征。此外，HMM还用于模拟生物序列，如蛋白质和DNA序列。

HMM模型比基础的马尔可夫模型多了一个观测概率分布，其由初始概率分布、状态转移概率分布和观测概率分布确定，因此可以用三元符号表示。

  • 初始概率分布（$\pi$）：表示最初处于各个状态的概率集合；
  • 状态转移概率矩阵（A）：表示从一个隐藏状态转移到另一个隐藏状态的概率；
  • 观测概率矩阵（B）：表示在给定观测状态下各隐藏状态的概率。

image-20240325203951026

举个例子：还是刚在的天气案例，只是难度加大了，现在这个天气情况我们没有办法去直接观测，是一个隐藏状态，我们只能够直接观测到海藻的状态【Dry(干燥), Dryish(稍干), Damp(湿润), Soggy(浸水)】，而海藻的状态跟天气有一定的关系。

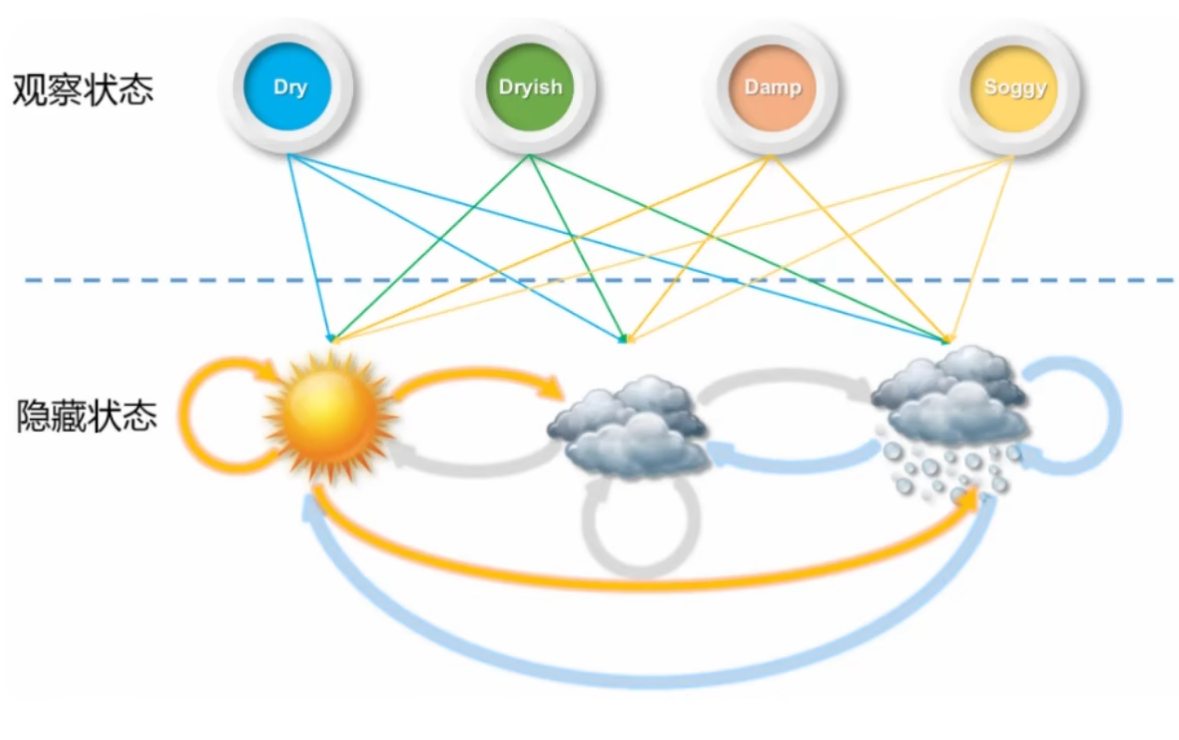
image-20240325204847761

这个时候和前面的基础的马尔可夫模型案例相比，还需要已知一个观测概率矩阵，也就是海藻的状态和天气之间具体有什么关联：

观测概率矩阵：

现在已知观测到未来三天的海藻状态为[Dry, Dryish, Dry]，求最有可能的隐藏状态序列.

求解方法：维特比算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 定义转移概率矩阵
A = np.array([[0.5, 0.375, 0.125],
         [0.25, 0.25, 0.5],
         [0.25, 0.375, 0.375]])

# 定义观测概率矩阵
B = np.array([[0.60, 0.20, 0.15, 0.05],
             [0.25, 0.25, 0.25, 0.25],
             [0.05, 0.10, 0.35, 0.50]])

# 定义初始概率矩阵
pi = np.array([0.8, 0.1, 0.1])

# 定义观测序列
O = np.array([0, 1, 0])
1
2
3
# 时刻1初始的隐藏状态概率为pi
i_1 = pi * B[:, O[0]]  # 时刻1的隐藏状态
i_1
array([0.48 , 0.025, 0.005])

1
2
3
4
# 第二天隐藏状态矩阵
h_1 = i_1@A  # 时刻2的初始隐藏状态
i_2 =  h_1.max() * B[:, O[1]]  # 时刻2的隐藏状态
i_2
array([0.0495  , 0.061875, 0.02475 ])

1
2
3
4
# 第三天隐藏状态矩阵
h_2 = i_2@A  # 时刻3的初始隐藏状态
i_3 = h_2.max() * B[:, O[2]]  # 时刻3的隐藏状态
i_3
array([0.02784375, 0.01160156, 0.00232031])

1
2
3
# 汇总所有时刻的隐藏状态矩阵
I = np.stack([i_1, i_2, i_3], axis=1)
I
array([[0.48      , 0.0495    , 0.02784375],
       [0.025     , 0.061875  , 0.01160156],
       [0.005     , 0.02475   , 0.00232031]])

1
2
# 求出最大的概率组合
I.argmax(axis=0)
array([0, 1, 0], dtype=int64)

定义维特比算法求解函数

求解任务模式

已知：

  • HMM模型的完整参数（转移概率矩阵A，观测状态矩阵B，初始概率矩阵pi）
    求解：
  • 指定观测状态序列$O_i$下隐藏状态序列$I_j$出现概率最大的结果。
1
2
3
4
5
6
7
8
9
10
def viterbi(A, B, pi, O):
    result = []
    for t in range(len(O)):
        if t == 0:
            result.append(pi * B[:, O[t]])
        else:
            result.append((result[t-1]@A).max() * B[:, O[t]])
    result = np.stack(result, axis=1)
    cut_result = result.argmax(axis=0)
    return cut_result
1
viterbi(A, B, pi, O)
array([0, 1, 0], dtype=int64)

使用监督学习训练HMM

将问题抽象出来即：已知观测状态序列（O）和隐藏状态序列（I），如何求出对应的HMM模型（$\lambda\{\pi, A, B\}$）？

生成数据

为了简单起见，直接使用前面的HMM模型训练数据。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def random_data(T):
    # 定义HMM模型
    # 定义转移概率矩阵
    A = np.array([[0.5, 0.375, 0.125],
         [0.25, 0.25, 0.5],
         [0.25, 0.375, 0.375]])

    # 定义观测概率矩阵
    B = np.array([[0.60, 0.20, 0.15, 0.05],
                 [0.25, 0.25, 0.25, 0.25],
                 [0.05, 0.10, 0.35, 0.50]])

    # 定义初始概率矩阵
    pi = np.array([0.8, 0.1, 0.1])
    
    # 定义隐藏状态序列
    I = []
    # 定义观测状态序列
    O = []
    
    # 循环时间步
    for t in range(T):
        if t == 0:
            idx = np.random.choice(len(pi), p=pi)
        else:
            idx = np.random.choice(len(pi), p=A[:, idx])  # 在前一个时间步隐藏状态为idx的基础上求现在时间步的隐藏状态
        I.append(idx)
        O.append(np.random.choice(B.shape[1], p=B[idx]))  # 用当前时间步的隐藏状态生成当前观测状态
    return I, O
1
random_data(10)
([2, 1, 2, 1, 0, 0, 2, 1, 1, 2], [3, 0, 3, 0, 0, 1, 3, 0, 0, 2])

1
2
3
4
5
6
7
8
9
10
11
12
13
# 定义数据量
data_size = 1000
# 定义时间步
T = 1000
# 生成样本数据
I = []
O = []
for i in range(data_size):
    i, o = random_data(T)
    I.append(i)
    O.append(o)
I = np.stack(I, axis=0)
O = np.stack(O, axis=0)

初始化参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 计算观测状态O_num和隐藏状态i=I_num
O_num = O[0].max() + 1
I_num = I[0].max() + 1

# 定义状态转移矩阵
A = np.zeros((I_num, I_num))


# 定义观测矩阵
B = np.zeros((I_num, O_num))


# 定义初始状态
pi = np.zeros(I_num)

开始计算

1
2
3
4
# 计算初始状态
for i in range(I_num):
    pi[i] = (I[:, 0] == i).mean()
pi
array([0.807, 0.098, 0.095])

1
2
3
4
5
6
7
8
9
# 计算状态转移矩阵
for n in range(data_size):  # 遍历数据
    for t in range(T-1):  # 遍历时间步
        for i in range(I_num):  # 遍历行数
            for j in range(I_num):  # 遍历列数
                    if I[n, t] == i and I[n, t+1] == j:
                        A[j, i] += 1  # 计数
A /= A.sum(axis=1, keepdims=True)
A
array([[0.50096283, 0.37414269, 0.12489448],
       [0.25011337, 0.25012538, 0.49976125],
       [0.25004353, 0.37500375, 0.37495272]])

1
2
3
4
5
6
7
8
9
# 计算观测矩阵
for n in range(data_size):  # 遍历数据
    for t in range(T):  # 遍历时间步
        for i in range(I_num):  # 遍历行数
            for j in range(O_num):  # 遍历列数
                if I[n, t] == i and O[n, t] == j:
                    B[i, j] += 1  # 计数
B /= B.sum(axis=1, keepdims=True)
B
array([[0.59910993, 0.19991908, 0.15019779, 0.0507732 ],
       [0.24941232, 0.25002477, 0.25091343, 0.24964949],
       [0.04929884, 0.10106142, 0.34963224, 0.5000075 ]])

计算成功！经过和原始数据对比发现相似度很高。

使用HMM实现中文分词任务

在中文分词任务中，观测状态为字，隐藏状态为每个字为BEMS中的一个状态。

  • B：词语开始
  • E：词语结束
  • M：词语中间字
  • S：孤立的单个字称为一个词语
1
from tqdm import tqdm

读取数据

1
2
3
4
with open('../data/icwb2-data/training/pku_training.utf8', 'r', encoding='UTF-8') as f:
    data = f.readlines()
data = [i.strip() for i in data if len(i.strip()) > 0]  # 注意原始数据中存在空数据，也需要删除
len(data)
19054

处理数据

按照BEMS方式标记数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
I = []  # 存储隐藏状态
O = []  # 存储观测状态
for string in data:
    i = []
    o = []
    string_words = string.split(' ')
    string_words = [i for i in string_words if len(i) > 0]  # 删除产生的空字符串
    for string_word in string_words:
        if len(string_word) == 1:
            i.append(3)
            o.append(ord(string_word))  # ord方法将汉字转化为unicode中的数值
        else:
            i.append(0)
            i.extend([2]*(len(string_word) - 2))
            i.append(1)
            o.extend([ord(i) for i in list(string_word)])
    I.append(i)
    O.append(o)

训练HMM模型

现在和前面的监督学习训练HMM一样，已知观测状态链和隐藏状态链。同样可以求出对应的HMM模型。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 计算观测状态O_num和隐藏状态i=I_num
O_num = max(max(O)) + 1
I_num = max(max(I)) + 1

# 定义状态转移矩阵
A = np.zeros((I_num, I_num))


# 定义观测矩阵
B = np.zeros((I_num, O_num))


# 定义初始状态
pi = np.zeros(I_num)
1
2
3
4
5
6
# 计算初始状态
for i in range(I_num):
    for j in range(len(I)):
        pi[i] += (I[j][0] == i)
pi = pi / pi.sum()
pi
array([0.63456492, 0.        , 0.        , 0.36543508])

1
2
3
4
5
6
7
8
9
# 计算状态转移矩阵
for n in tqdm(range(len(I))):  # 遍历数据
    for t in range(len(I[n])-1):  # 遍历时间步
        for i in range(I_num):  # 遍历行数
            for j in range(I_num):  # 遍历列数
                    if I[n][t] == i and I[n][t+1] == j:
                        A[j, i] += 1  # 计数
A /= A.sum(axis=1, keepdims=True)
A
100%|██████████████████████████████████████████████████████████████████████████| 19054/19054 [00:05<00:00, 3230.11it/s]

array([[0.        , 0.49242151, 0.        , 0.50757849],
       [0.85322422, 0.        , 0.14677578, 0.        ],
       [0.6543287 , 0.        , 0.3456713 , 0.        ],
       [0.        , 0.57792637, 0.        , 0.42207363]])

1
2
3
4
5
6
7
8
9
# 计算观测矩阵
for n in tqdm(range(len(I))[:1000]):  # 遍历数据，由于数据量比较大，所以在计算观测矩阵时，仅选择前1000条数据进行训练，要想得到更好的效果可以将训练数据量增大
    for t in range(len(I[n])-1):  # 遍历时间步
        for i in range(I_num):  # 遍历行数
            for j in range(O_num):  # 遍历列数
                if I[n][t] == i and O[n][t] == j:
                    B[i, j] += 1  # 计数
B /= B.sum(axis=1, keepdims=True)
B
100%|██████████████████████████████████████████████████████████████████████████████| 1000/1000 [43:43<00:00,  2.62s/it]

array([[0., 0., 0., ..., 0., 0., 0.],
       [0., 0., 0., ..., 0., 0., 0.],
       [0., 0., 0., ..., 0., 0., 0.],
       [0., 0., 0., ..., 0., 0., 0.]])

这里可以自己手动去修改对数据量的循环[:1000]如果将这个内容删除，则会对所有样本进行训练，预计消耗时间14h。

1
2
# 存储中间结果
np.savez('hmm_model_params_epoch1000.npz', A=A, B=B, pi=pi)

使用HMM进行分词

前面我们已经将HMM模型训练完毕，接下来使用训练好的HMM模型，对指定序列进行分词。

这里就可以使用到维特比算法，找到指定观测序列最大概率的隐藏序列。

1
test_text = '我们即将以丰收的喜悦送走牛年，以昂扬的斗志迎来虎年。我们伟大祖国在新的一年，将是充满生机、充满希望的一年。'
1
2
3
# 将指定文本转化为观测序列
test_text_ord = [ord(i) for i in list(test_text)]
print(len(test_text_ord))
53

1
2
# 使用维特比算法求解最大概率的隐藏序列结果
cut_result = viterbi(A, B, pi, test_text_ord)
1
2
3
# 将分词结果还原到句子中，在所有的1和3后面加上|
new_string = ''.join(char + '|' if value in [1, 3] else char for char, value in zip(test_text, cut_result))  
new_string
'我们|即将|以|丰收的|喜悦|送|走|牛年|，|以|昂扬|的|斗|志|迎来|虎年|。|我们|伟大祖国|在|新的|一|年|，|将|是|充满|生机、|充满|希望|的|一|年|。|'

编写成函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def cut(string, A=None, B=None, pi=None, sep=' ', model_params_path=None):
    # 要直接指定HMM的三个参数，要么就指定缓存的npz文件路径，如果都不指定就报错
    if (model_params_path == None) and np.any(A == None):
        raise ValueError('请指定模型参数！')
    if model_params_path:
        model_file = np.load(model_params_path)
        A, B, pi = model_file['A'], model_file['B'], model_file['pi']
    # 将指定文本转化为观测序列
    test_text_ord = [ord(i) for i in list(string)]
    # 使用维特比算法求解最大概率的隐藏序列结果
    cut_result = viterbi(A, B, pi, test_text_ord)
    # 将分词结果还原到句子中，在所有的1和3后面加上空格
    new_string = ''.join(char + sep if value in [1, 3] else char for char, value in zip(string, cut_result))  
    return new_string

使用100个样本的训练参数

1
cut('台湾是中国领土不可分割的一部分', sep='|', model_params_path='hmm_model_params_epoch100.npz')
'台湾|是|中国|领土|不|可分|割|的|一部|分|'

使用1000个样本的训练参数

1
cut('台湾是中国领土不可分割的一部分', sep='|', model_params_path='hmm_model_params_epoch1000.npz')
'台湾|是|中国|领土不|可分割的|一|部|分'

由于模型训练比较耗时，这里我使用了1000个样本进行训练时，消耗的时间是43分钟，训练的CPU是Inter i7-11th，大家要想得到更好的效果可以自行尝试增加训练样本，如果将所有样本全部放入模型中进行训练可能会消耗14个小时左右。

-------------本文结束感谢您的阅读-------------